B- tree, B+ tree에 대하여. 장단점, 특징, 삽입/삭제, 검색..

오늘은 이진 트리에서 발전된 형태인 B tree 친구들에 대해서 알아볼까 한다.

 

이진 트리란?

• 각각의 노드가 최대 두 개(0개, 1개, 2개)의 자식 노드를 가지는 트리 자료구조

• 자세하게는 Full 이진 트리, 완전 이진 트리, 균형 이진 트리, 이진 탐색 트리 등이 존재한다.
  • 모든 노드가 0개 또는 2개의 자식 노드를 갖는 full 이진 트리,
  • full 이진 트리 중 leaf node가 꽉 찬 트리를 포화 이진 트리,
  • 마지막 레벨을 제외한 모든 레벨에서 순서대로 (왼쪽->오른쪽)node가 채워진 트리를 완전 이진 트리,
  • 이진 트리이면서 다음과 같은 속성을 가지는 이진 탐색 트리,
    • 노드에 저장된 키는 유일하다.
    • 부모 키는 왼쪽 자식 키보다 크다.
    • 부모 키는 오른쪽 자식 키보다 작다.
    • 왼쪽, 오른쪽 서브트리도 이진 탐색 트리이다.
  •  leaf node들의 레벨 차이가 최대 1레벨까지 나는 균형 이진 트리

---

여기서 주목해야 할 트리는 바로 '균형 이진 트리' 이다.

균형 이진 트리는 AVL 트리, red-black 트리, B(+, -, *) tree 등에서 사용되기 때문이다.

 

그럼 자세한 버전으로 균형 이진 트리란 무엇일까?

: 균형 이진 트리란, '높이 균형'이 맞춰진 트리를 의미한다.

 

높이 균형?

: 즉, 삽입과 삭제가 일어나는 경우 그 높이(루트에서부터 내려갈 수 있는 최대 레벨)을 작게 유지하는 노드 기반 이진 탐색 트리를 의미한다.

해당 자료구조는 변경이 가능한 정렬 리스트의 효율적인 구현이며, associative array(연관 배열), priority queue(우선순위 큐), 집합(set)과 같은 여러 추상 자료구조로 쓰인다.

​

균형 이진 트리는 탐색 시 O(logN)의 시간 복잡도를 가지는데, 당연히 '완전한 균형'은 가져다 줄 수 없다. (NP문제.. 기억하시죠?)

 

그렇지만 트리의 속도는 트리에 깊이에 따라 결정되고, 따라서 시간 복잡도를 줄여 효율적으로 트리를 사용하기 위해

트리 깊이의 균형을 맞추어 검색,삽입,삭제에서 시간복잡도를 O(logN)의 성능으로 만들어주는 것이 중요하다.

---

1. B-tree

 

B-tree는 균형 이진 탐색 트리의 일종이다.

'균형' 트리이기 때문에 루트로부터 리프까지의 거리가 일정하고,

'탐색' 트리이기 때문에 데이터(키)는 정렬된 상태를 유지하고 있다.

 

'차수'라는 개념이 존재하는데, 하나의 노드가 여러개의 키와 자식을 가질 수 있기 때문이다.

N차 B-tree( N Order B-tree) :  N-1개의 키와 최대 N개의 자식을 가질 수 있는 B-tree

 

따라서, 이진 트리보다 훨씬 많은 데이터를 효율적으로 저장할 수 있다는 장점이 있다.

파란색 : 각 노드의 key

빨간색 : 자식 노드를 가리키는 포인터

 

그림을 보면 알 수 있듯이, key들은 항상 정렬되어 있으며

이진 탐색 트리와 같이 왼쪽 자식들은 부모보다 작은 값을, 오른쪽 자식들은 부모보다 큰 값을 가진다.

 

[검색]

루트에서 시작하여 하향식으로 검색 진행. (검색 대상 : k)

1. 루트 노드에서 시작하여 key들을 순회하면서 검사
   1-1. 만일 k와 같은 key를 찾았다면 검색 종료
   1-2. 검색하는 값과 key들의 대소관계 비교. key들 사이에 k가 들어간다면 해당 key들 사이의 자식노드로 하향
2. 1을 리프노드에 도달할 때까지 반복

ex) 18 검색 : 루트 -> 가운데->오른쪽->찾음!

 

[삽입]

하향식으로 절절한 리프 노드를 찾고, 필요 시 상향식으로 노드 분할.

1. 자료는 항상 리프(Leaf) 노드에 추가
2. 리프 노드의 선택은 ROOT 노드부터 시작해 하향식으로 탐색하며 결정
3. 선택한 리프 노드에 여유가 있다면 그냥 삽입. 여유가 없다면 분할
   • [ 노드 분할하는 방법 ]
   • 1. 오름차순으로 요소를 삽입. 우선 노드가 담을 수 있는 최대 key 개수를 초과한다.
   • 2. 중앙값에서 분할을 수행한다. 중앙값은 부모 노드로 병합하거나 새로 생성된다.
   • 3. 왼쪽 키들은 왼쪽 자식으로, 오른쪽 키들은 오른쪽 자식으로 분할된다.
   • 4. 부모 노드를 검사해서 또 다시 가득 찼으면 1~3을 반복한다.

ex) 9 삽입 : 루트 -> 왼쪽 -> 오른쪽 -> 7옆에삽입

ex) 13삽입 : 루트 -> 가운데 -> 왼쪽 -> 일단 맨 오른쪽 삽입. 11 12 13됨. 분할해야 한다.

-> 중앙값을 기준으로 분할해야 한다. 11 13을 자식으로, 12를 부모로 만든다.

-> 그럼 부모가 12 14 17이 되겠지? 다시 분할한다. 12 17을 자식으로, 14를 부모로 만든다.

-> 그럼 부모가 10 14 20이 되겠지? 다시 분할한다. 14를 부모로, 10 12를 자식으로 만든다.

끝

13 삽입 결과

 

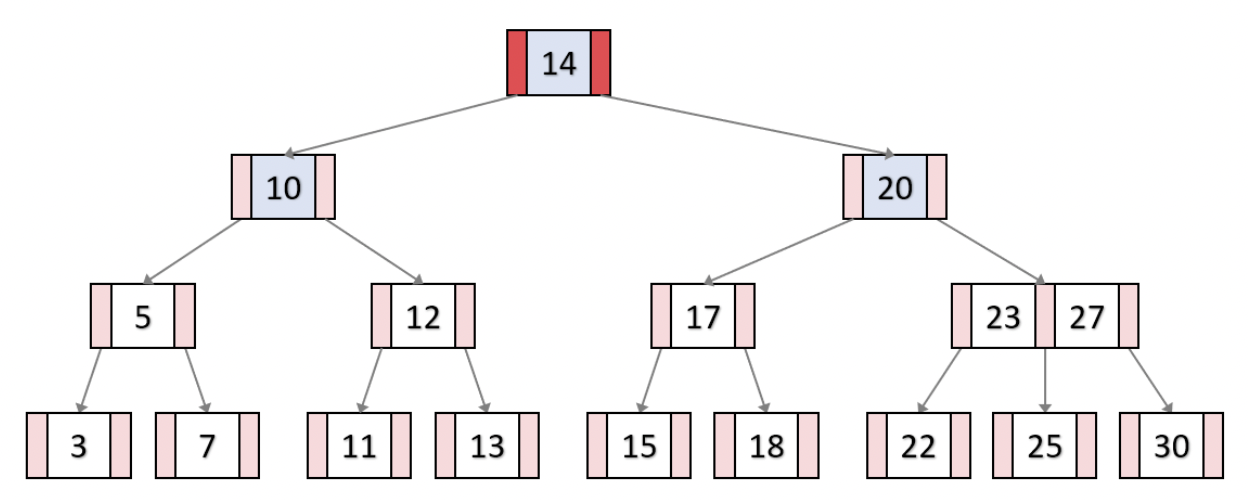
[삭제]

삭제할 키 : k

 삭제할 키가 있는 노드 검색, 키 삭제, (필요시)트리 균형 조정 으로 구성된다.

• inorder predecessor : 노드의 왼쪽 자손에서 가장 큰 key
• inorder successor : 노드의 오른쪽 자손에서 가장 작은 key
• 부모 key: 부모노드의 key들 중 왼쪽 자식으로 본인 노드를 가지고 있는 key값 (단, 마지막 자식노드의 경우에는 부모의 마지막 key)

• 삭제 할 key가 leaf node에 있는 경우
  • 현재 노드의 키 개수가 최소 키 개수보다 클 때 : 삭제.
  • 왼쪽/오른쪽 형제 노드의 키 개수가 최소 키 개수보다 클 때 : 
    • 부모 key로 삭제할 키 대체.
    • 최소키 개수 이상의 키를 가진 형제 노드가 왼쪽 형제라면 가장 큰 값을, 오른쪽 형제라면 가장 작은 값을 부모key로 대체
  • 왼쪽/오른쪽 형제 노드의 키 개수가 최소 키 개수이고, 부모노드 키 개수가 최소 개수보다 클 때:
    • k를 삭제한 후, 부모key를 형제 노드와 병합
    • 부모노드의 key개수를 하나 줄이고, 자식 수 역시 하나를 줄여 B-Tree를 유지 (균형 맞추기)
  • 자신과 형제, 부모 노드 키 개수가 모두 최소 키 개수일 때
    • 부모노드의 key개수를 하나 줄이고, 자식 수 역시 하나를 줄여 B-Tree를 유지 (균형 맞추기)
• 삭제 할 key가 leaf node가 아닌 노드에 있는 경우
  • 현재 노드의 inorder predecessor 또는 inorder successor와 k의 자리를 바꾼다.
    • 삭제할 key가 leaf node에 있는 경우로 돌아감.
    •  

ex) 12 삭제 : 그냥 지우면 됨.

ex) 15 삭제 : 왼쪽 노드 키가 최소 키 개수 이상이다.  

따라서 왼쪽 노드에서 가장 큰 값인 14를 15가 있던 자리에 대체한다. 그 다음 그냥 삭제하면 됨.

결과

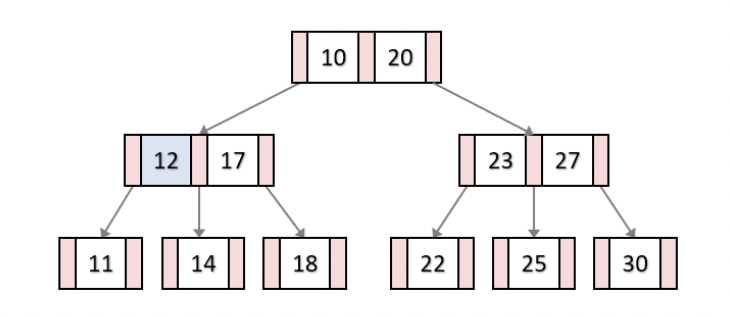
ex) 18 삭제 : 형제 노드는 최소 키 개수고 부모 노드는 최소 개수 이상이다.

따라서 18을 그냥 삭제하고, 부모 노드 키인 17일 14옆에 붙인다. 

결과

---

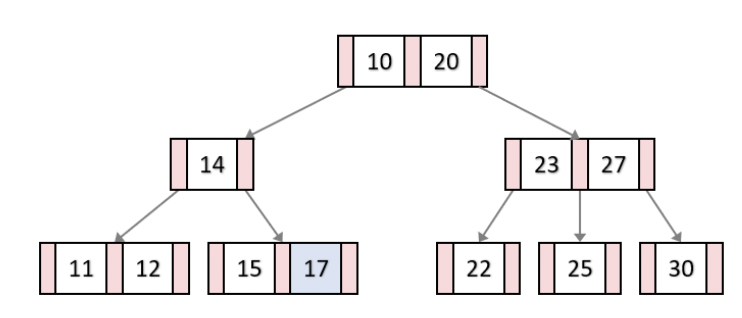
2. B+tree

 

B+tree는 균형 이진 탐색 트리의 일종이다.

탐색을 하려면 노드를 찾아서 이동해야되는 B-tree와 다르게,

 B+Tree는 같은 레벨의 모든 키값들이 정렬되어 있고, 형제 노드들은 연결리스트로 이어져있다.

따라서 탐색 시 매우 유리하다.

 

실제 DB의 인덱싱은 B+tree로 이루어져있다고 한다. 

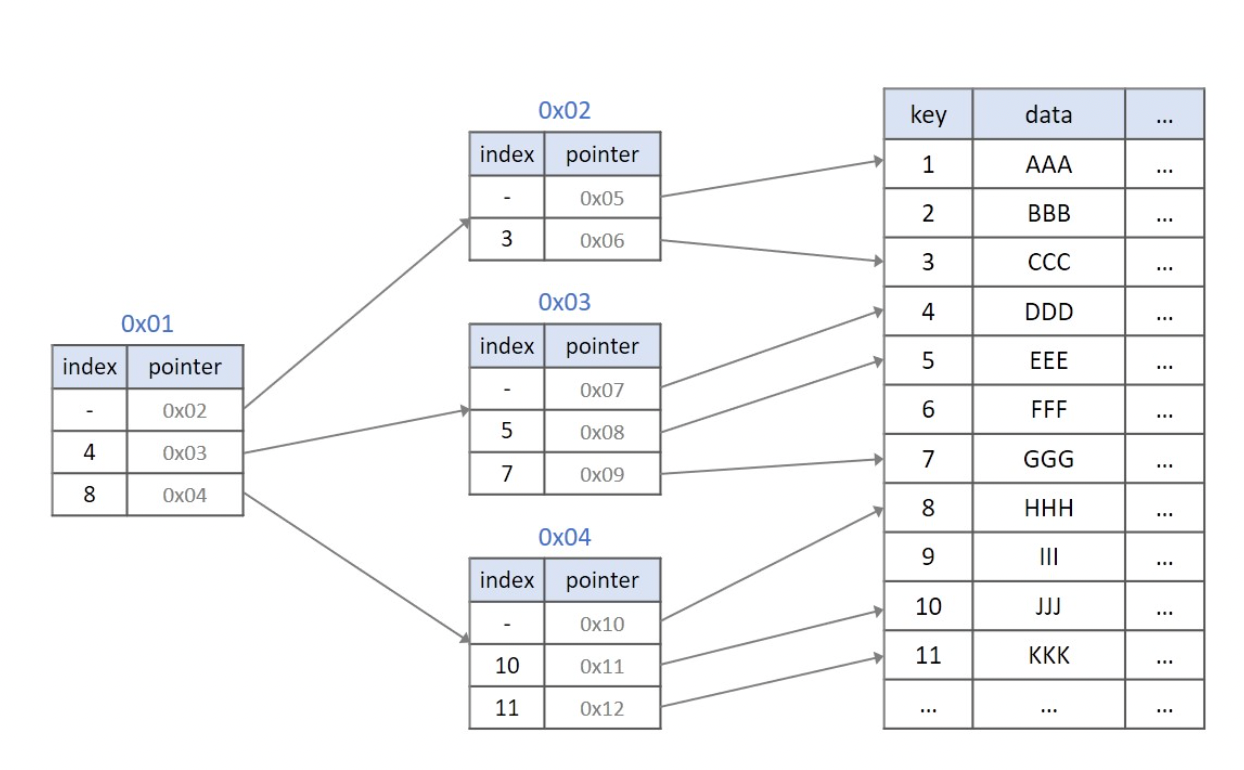
위 인덱싱을 B+tree로 나타내면 다음과 같다.

 

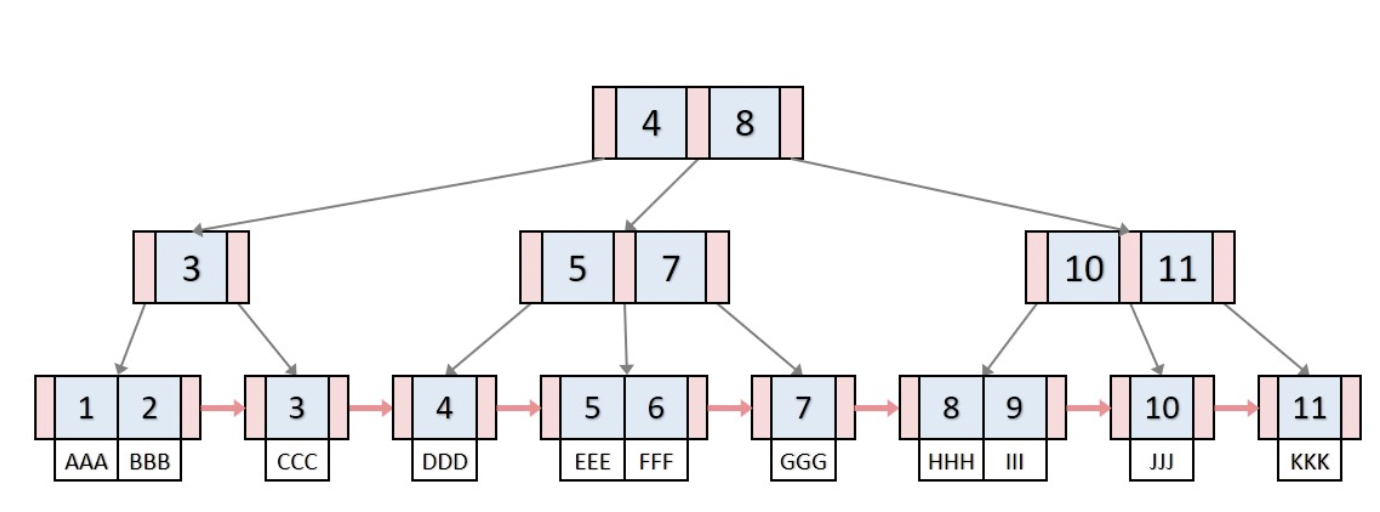
B+tree의 leaf node는 데이터 노드라고도 부르는데, 연결 리스트로 이어져있는 것을 확인할 수 있다.

leaf node가 아닌 노드는 인덱스 노드라고 하는데, 다음 노드를 가리킬 수 있는 포인터 주소가 존재한다.

 

따라서 키 값 중복이 가능하고, (인덱스와 데이터에서) 데이터 검색을 위해서는 반드시 leaf node까지 가야한다.

 

[검색]

B-tree와 동일

 

[삽입]

하향식으로 절절한 리프 노드를 찾고, 필요 시 상향식으로 노드 분할.

1. 자료는 항상 리프(Leaf) 노드에 추가
2. 리프 노드의 선택은 ROOT 노드부터 시작해 하향식으로 탐색하며 결정
3. 선택한 리프 노드에 여유가 있다면 그냥 삽입. 여유가 없다면 분할
   • 노드의 분열이 있을 때는 중간 key값이 부모 노드로 올라가고, 새로 분열된 노드에도 포함되어야 한다.
   • 새 노드는 leaf node의 연결 리스트에도 삽입되어야 한다.
   • 분열이 일어나는 노드가 leaf 노드라면 ??
     • 왼쪽 자식노드와 오른쪽 자식 노드를 이어줘 연결리스트 형태를 유지해야 한다.

ex) 16 삽입 : 삽입 삭제는 리프 노드에서만 이루어진다는 것을 기억해야 한다. 17 앞에 16을 붙이고 부모 키를 갱신한다.

leaf node에서 개수를 초과한 경우 어떻게 분할하는지:

ex) 18 삽입 : 자리를 찾아가다 보면 리프 노드가 16 17 18이 된다. 노드를 16 1718로 분할하고 오른쪽 노드의 가장 작은 값을 부모 키로 설정한다. 나머지 연결 리스트를 연결한다. 리프 노드가 아닌 노드를 분할할 때는 중간 노드를 부모로 보낸다. B-tree와 같음.

 

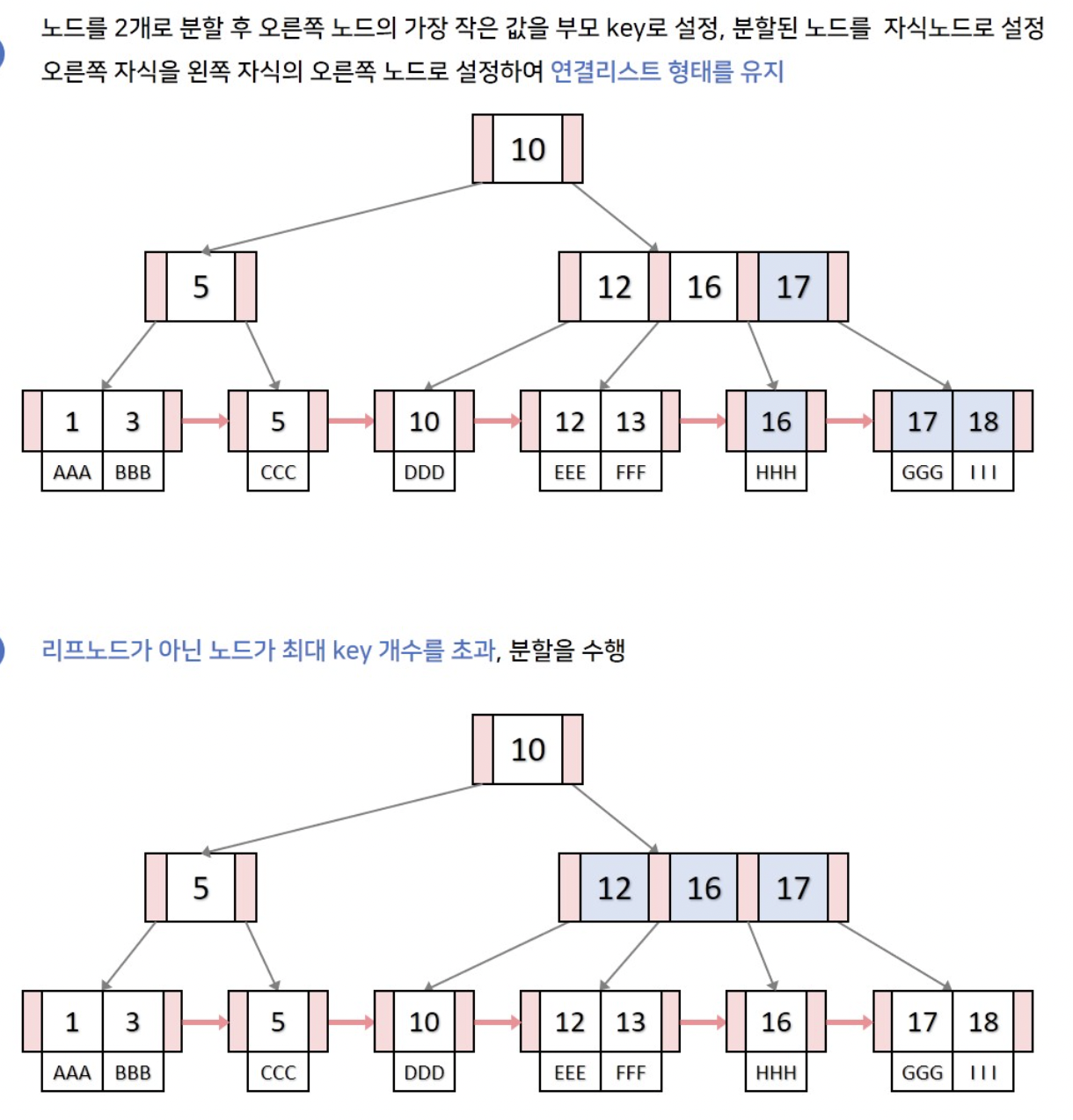
[삭제]

B-tree와 유사하지만, 삭제할 키는 무조건 리프 노드에 존재해야 한다.

삭제할 키를 삭제하기 위해 검색하는 과정에서 인덱스 노드에 리프 노드랑 같은 값이 있을 수 있다.

• 재배치와 병합이 필요하지 않을 때는 leaf 노드에서만 삭제된다.
• Index 부분은 다른 key 값을 찾는데 사용될 수 있기 때문에 leaf node의 값이 삭제되어도 삭제하지 않는다.
• 재배치할 경우 index 부분의 node의 key 값은 변하지만 tree 구조는 변하지 않는다.
• 병합을 할 경우 index 부분에서도 key 값을 삭제한다.

(삭제할 키가 리프 노드의 처음 키인 경우는 항상 인덱스 노드 내에 같은 값이 존재할 수 밖에 없다)

B-tree와 B+tree의 공통점
---------------------------------------------------------

공통점
			모든 leaf의 depth가 같다.
			각 노드에는 k/2~k개의 키가 들어있어야 한다.
			삽입 시 최대 키 개수를 넘어가면 분할한다.
			삭제 시 최소 키 개수를 만족하지 못하면 재배치하거나 병합을 한다.

B-tree와 B+tree의 차이점
---------------------------------------------------------

	B-tree	B+tree
데이터 저장	리프 노드, 인덱스 노드 모두 데이터 저장 가능 (모든 노드가 키마다 데이터를 가짐)	리프 노드에만 데이터 저장 가능
full scan 검색 속도	모든 노드 탐색	리프 노드에서 선형 탐색
키 중복	없음	있음(리프 노드와 인덱스 노드에 1개씩)
검색	자주 access 되는 노드를 루트 노드 가까이 배치할 수 있고, 루트 노드에서 가까울 경우, 브랜치 노드에도 데이터가 존재하기 때문에 빠르다. 즉 best case에 대해서 루트에서 끝낼 수도 있다.	무조건 리프 노드까지 가야 데이터가 존재한다. 비교적 느릴 수 있다.
삽입,삭제	모든 노드에서 이루어질 수 있다.	리프 노드에서만 이루어진다.
연결리스트	없음	리프 노드가 연결 리스트
트리 높이	높음	낮음
옆에 있는 리프 노드 검사	다시 루트 노드부터 검사해야 한다. (시간 오래 걸림)	모든 리프 노드가 연결 리스트의 형태를 띄고 있어, 옆에 있는 노드를 검사할 때도 선형 검사를 수행할 수 있다
장점	1. 삽입, 삭제 후에도 균형이 유지된다. 2. 균등한 탐색 속도를 보장할 수 있다. (logN)	1. 리프 노드를 제외하고 데이터를 담아두지 않기 때문에 메모리를 더 확보함으로써 더 많은 key들을 수용할 수 있다. 2. 하나의 노드에 더 많은 key들을 담을 수 있기에 트리의 높이는 더 낮아진다. 3. B+tree는 리프 노드에 데이터가 모두 있기 때문에 한 번의 선형탐색만 하면 되기 때문에 B-tree에 비해 빠르다. 4. 블럭 사이즈(노드 사이즈)를 더 많이 이용할 수 있다.
단점	1. 순차 탐색 시 중위 순회를 하기 때문에 비효율적이다. 2. 삽입, 삭제 시 균형 유지를 위해 복잡한 연산이 수행된다.	1. 무조건 leaf node까지 가야 하기 때문에 비효율적인 경우가 있다.

 

참고했어요~

https://ssocoit.tistory.com/217

[자료구조] 간단히 알아보는 B-Tree, B+Tree, B*Tree

https://velog.io/@emplam27/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EA%B7%B8%EB%A6%BC%EC%9C%BC%EB%A1%9C-%EC%95%8C%EC%95%84%EB%B3%B4%EB%8A%94-B-Tree

[자료구조] 그림으로 알아보는 B-Tree

https://velog.io/@emplam27/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EA%B7%B8%EB%A6%BC%EC%9C%BC%EB%A1%9C-%EC%95%8C%EC%95%84%EB%B3%B4%EB%8A%94-B-Plus-Tree

[자료구조] 그림으로 알아보는 B+Tree